Huvudskillnad: I matematik används en ekvation för att beteckna jämlikheten mellan två uttryck. En funktion å andra sidan är i mycket mer komplex än en ekvation. En funktion används för att beteckna en relation mellan en uppsättning ingångar och en uppsättning motsvarande utgångar.

En ekvation och en funktion är två av de grundläggande grundvalarna för algebra, ett ämne under matematik. Båda kan vara ganska komplexa, men i sin grundläggande form kan de vara förvirrade som varandra. Huvudskillnaden mellan en ekvation och en funktion är det faktum att en ekvation brukar handla om en enda ingång, medan en funktion kan ha många ingångar.

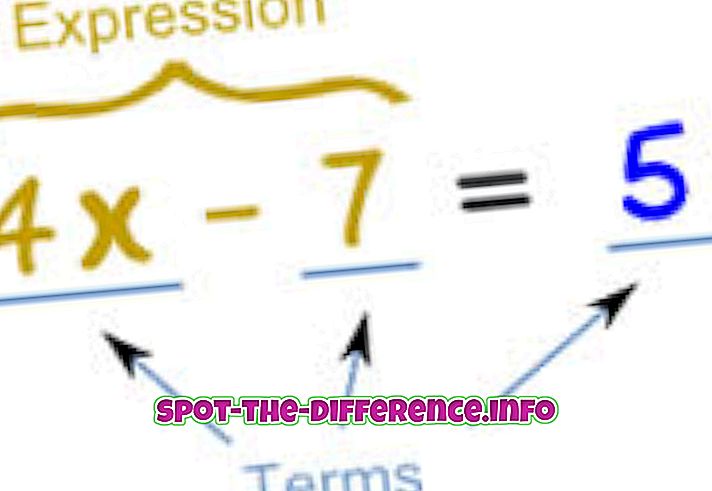
I matematik används en ekvation för att beteckna jämlikheten mellan två uttryck. I huvudsak skrivs en ekvation som ett uttryck som liknar ett annat uttryck. Till exempel: x + 2 = 5. Detta betyder att det som är x, om du lägger till 2 till det, kommer att vara lika med 5. Därför kan vi lösa ekvationen för x, vilket är 3, som 3 + 2 = 5.

Ekvationer kan vara mer komplexa än det och kan innefatta mer än en variabler, såsom x, y, z, etc. i en enda ekvation. Till exempel: 3x + 2y - z = 4. Men varje alfabet kommer att motsvara ett nummer. I detta fall x = 1, y = 2 och z = 3.

Därav,

3x + 2y - z = 4 blir

3 (1) + 2 (2) - 3 = 4 vilket är

3 + 4 - 3 = 4 väsentligen

4 = 4

En funktion å andra sidan är i mycket mer komplex än en ekvation. En funktion används för att beteckna en relation mellan en uppsättning ingångar och en uppsättning motsvarande utgångar. I huvudsak bör en ingång ge en enda utgång. En funktion är ett förhållande mellan två variabler. Till exempel: f (x) = x + 2. Enligt denna funktion, oavsett vilken ingång som helst, kommer det att ge dig en enda utgång, vilket kommer att vara input plus 2. Låt oss lösa den här funktionen:

Inmatning	Fungera	Produktion
x	f (x) = x + 2	f (x)
1	1 + 2	3
2	2 + 2	4
3	3 + 2	5
4	4 + 2	6
5	5 + 2	7

Och så vidare…

Funktioner har olika tillämpningar inom matematik, fysik, datavetenskap, etc. De kan sträcka sig från en enkel funktion, som angivits ovan, till komplexa formler eller algoritmer. En funktion kan ses som en maskin som ger en utgång för en ingång, och att utsignalen på något sätt är relaterad till ingången.

En funktion har alltid tre delar: ingången, förhållandet och utgången. Den klassiska sätten att skriva en funktion är med "f (x) = ...", där x betecknar ingången och f (x) betecknar utgången.

Som nämnts ovan är huvudskillnaden mellan en ekvation och en funktion att en ekvation vanligtvis bara har en ingång som kommer att leda till att uttrycken är lika. En funktion har olika ingångar, vilka kommer att ge en effekt.